A seabird in (early) flight position in Santa Cruz
English
I.
A few days ago, I listened to a podcast in which the two guests talked about "talent", and specifically about how to identify talent—the guests have recently written a book on this very topic.
Talent can be defined as a person doing something particularly well or have the potential to do so, or a particular trait, ability, or characteristic that is much better than what people usually possess; we can say “she is a talent” or “her talent is for mental calculation”.
Identifying talent when it is not yet fully expressed is challenging: those who are involved in sports, as I have always been, can recall dozens of promising young athletes whose careers evaporated like snow in July when the boys hit puberty, or found a girlfriend who drove them crazy, or decided to switch from goal shooting to shooting up drugs.
There are also other traits—either physical (resistance to injury, for example) or psychological—that are not tested when the kids are still young; it is difficult to assess how well the kids, as adults, will be able to withstand the pressure of competition when the other players are also professionals—when the promising kid is ten times better than the other competitors, the pressure of competition is simply not there.
For a once-in-a-generation talent like Lionel Messi, hundreds of once-in-a-generation talents never blossomed because they collapsed under the pressure of competition. Or because they get injured by the mere blowing of a kiss in the direction of their calves.
II.
At the time of my research in evolutionary biology, one trait or characteristic that particularly interested me was "individual quality." The concept of individual quality is used to explain inter-individual heterogeneity in performance, which means, simply put, that there are individuals who do better than others, which are then said to be of "higher quality." But while doing better (making more children, surviving for more years, being bigger and faster) can be observed, being better—having the potential to do better than others—is often difficult to observe.
When observing a phenomenon or process, it is always useful—or rather necessary, but let's start with the more subtle "useful"—to study its distribution (what is the frequency of the measures, of the events?), thanks to which we can observe the realization of a certain phenomenon in the context of what can happen and how likely it is to happen.
For example, we may thing that producing offspring is not something particularly exceptional, but in many species, including humans over millennia, only a fraction of individuals who reach sexual maturity actually reproduce, that is, give birth to offspring that then survive to sexual maturity.
Talking about other species, only about 3 out of 10 of the adult seabirds I have had the pleasure of studying in my biological research are expected to successfully reproduce—I used the adverb "successfully" because some eggs get fertilized, but no chicks come out of the eggs or the chicks die immediately (or are killed by their parents!) after hatching: there is reproduction, but not a successful one.
To offer a more easily observable example, we cannot say whether a man who is five feet four inches tall is tall or short except in the context of the frequency of a particular height in the population: a man who is five feet tall is short among the Dutch, but he is tall among the pygmies.
Most discussions about who is better (e.g., faster, taller, smarter) among groups of people go nowhere because the participants do not think in terms of distributions.
Saying “men are taller than women” is intuitively true, but that does not mean that every man is taller than every woman. The intuition is about the mean (men are on average taller than women) or the expectation that one has when thinking about a man and a woman taken at random, with the man expected to be taller than the woman.
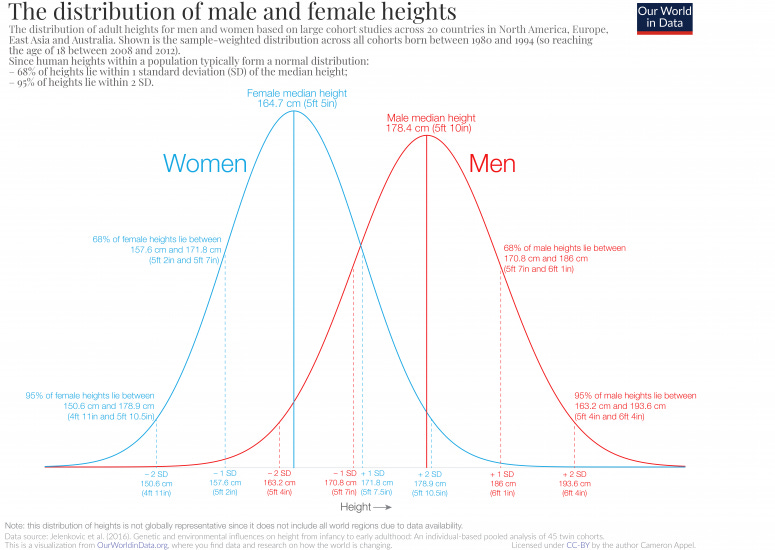
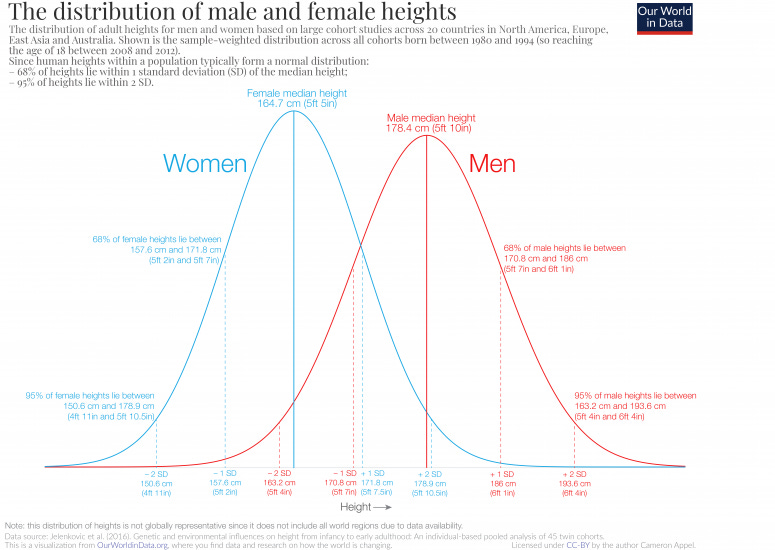
In the figure below, which I took from Our World in Data, refers to the height of adult men (red) and women (blue) born in North America, Europe, East Asia, and Australia between 1980 and 1994.
The two distributions overlap (and quite broadly overlap), which means that, in the region of overlap, the same height can be found for both men and women, although their probability of occurrence is different. For example, approximately only 2.5% of women are taller than 179 cm, but 50% of men are taller than 179 cm.
The collection of heights of men or women taken separately (not when taken together, in that case, we would observe a bimodal distribution) follow a normal distribution, which is a very common form, for mathematical reasons, of probability distribution.
The normal distribution is symmetric, which means that, say, people who are between 10% and 15% taller or between 10% and 15% shorter than the mean height appear in the population (which in this case is the collection of adult men and women) with the same frequency.
We can also say, because this is a property of normal distributions, that 95% of the heights are within 2 standard deviations of the mean. The standard deviation of a distribution is a measure of how the distribution is spread out, where larger standard deviations means wider distributions.
Since the mean height of men in North America, Europe, East Asia, and Australia born between 1980 and 1994 is 5ft 10in inches (178.4 cm) and the standard deviation is 3 inches (7.6 cm), it means that only 2.5% of adult males in the US are taller than 6ft 4 in (193 cm) and only 2.5% are shorter than 5ft 4in inches (163 cm).
The distribution of men's heights is more widespread than that of women; this is typically observed for a number of physical and behavioral traits, that is, the same trait is more variable in men than in women.
Normal (or pseudo-normal) probability distributions well describe the distribution of many common events or traits, but power-law distributions (or power-law-like, here I am more interested in intuition than in mathematical rigor) are also common. While a normal distribution is symmetric, thus implying that a proportional difference from the mean in either direction is equally likely (being shorter than 163 cm and taller than 193 is equally likely among men, since both quantities are 2 standard deviations away from the mean), a power-law distribution implies that small occurrences are common, while larger occurrences are rare.
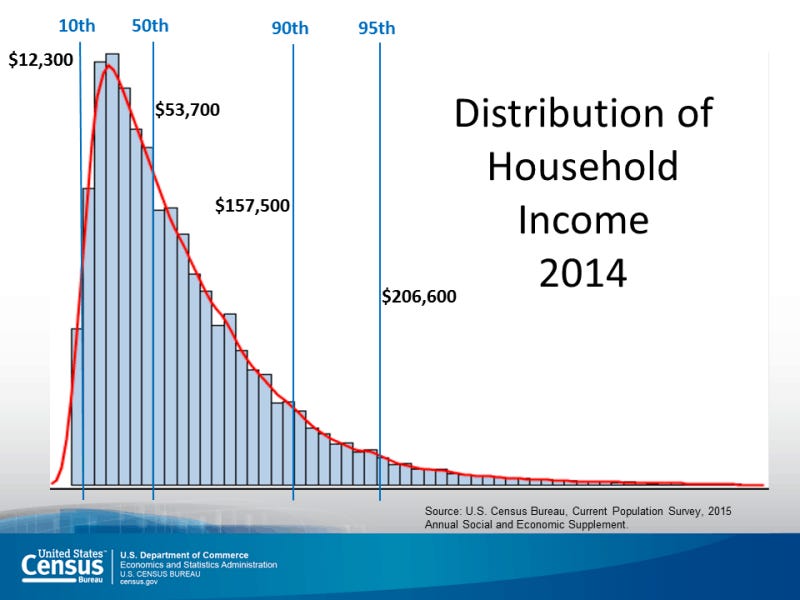
As shown in the figure below relative to the distribution of household income in the US in 2014, income or wealth follows a power-law distribution: there are very few billionaires and plenty of people with little money. And a power-law distribution also describes the frequency of the magnitude of earthquakes: there are many earthquakes whose occurrence can be detected only with special instruments, and very few earthquakes that raze a city to the ground.
Likewise, many women don’t reproduce at all or make 1 or 2 kids, and very few women make 15 or 20 kids through their lifetime. When I investigated the reproductive behavior of some populations of fish I was studying, I found that after a flood that killed most of the sexually mature fish, a couple of those fish was found to be responsible for more than 80% of the little fish that were produced one and two years after the flood, and a few other pairs of fish produced the remaining 20%: some do a lot and most do little.
All organisms, apart from some exceptions (see the eusocial behavior of bees), “desire” to reach sexual maturity and then reproduce—after losing their reproductive capability, due to senescence (using more common words we might say, “after getting old”) for example, they do little for the continuation of the species.
In fact, much research has been done to understand why women still survive for several years after entering menopause (or why menopause exists at all)—natural selection acts on traits that increase the fitness (i.e., the ability to survive, reach sexual maturity, and reproduce) of the individual or species, but it should not, in theory, act on traits that favor the survival of the individual after they have lost their reproductive capacity (or act to eliminate deleterious mutations in that late stage of life). For those interested in knowing more, I recommend reading up on the "grandmother hypothesis".
III.
It is commonly believed that talent, the "intrinsic talent" given to us by our parents and then modulated by our earliest life experiences, is normally distributed in the population (like height), but instead achievements follow a power-law distribution (like the magnitude of earthquakes), with many achieving nothing or almost nothing and others playing in the NFL for 12 years while winning quite a bit of rings and medals.
There are certainly substantial differences in ability or quality among people for a specific activity: some people are “naturally” better at drawing than others, for example. But some people are more talented than most of their peers in many activities and traits, some of which we may not be expect to be, at first glance, positively correlated (in general, there is a positive correlation between two measures when one increases when the other increases, but it does not necessarily mean that one is causing the other): being attractive and intelligent and generous is a good example. "Do you need anything else?" we might be tempted to ask those lucky people.
This is a bit counterintuitive, since for cultural reasons—and I would also say for a message common to all religions—we tend to believe that what is given in one aspect or quality is taken away from other aspects and qualities: we don't expect the beautiful woman or man to be brilliant and we expect the unfortunate person in a wheelchair to be, broadly speaking, a better person than someone who can walk.
But this is empirically not true: there are plenty of beautiful men and women who are also terrifically intelligent. And I add that I expect that combination to be more likely than both the combinations beautiful/dumb and bad-looking/brilliant, since the common “talent” or ingredient underpinning both “qualities” is “health”.
On the other hand, there are plenty of terrible people who have had the misfortune not only to be terrible, but also to be in a wheelchair: life is not fair, and "fairness" is a purely cultural concept. In fact, if we move the discussion from human beings to, say, lions, we would not say that we expect frail lions that have been crippled by a buffalo to be "wise," "kind," or "good listeners".
At the top level of any activity, and especially when the results are measurable (competitions of weight, seconds, distance, number of problems solved, the nod of approval of experts) and dependent only on the individual (no teamwork!), all competitors have “intrinsic talent”, likely a combination of genes and positive early life experience—I can train as much as I want, but I will never be as fast in a 100-meter race as a national-level competitor, I simply don’t have the genes for it. I can become better than I am (or better, I could have become better than I was), but the national level is outside my reach. Likewise, placing at the Math or Physics Olympics is impossible for people of not superior “intrinsic talent”, and I am unfortunately among them (but life is great anyway).
The problem when talking about “talent” or “quality” is that most discussions around those concepts are circular. I wrote about this issue in an old draft of a paper I published on kittiwake (a common seabird) life histories.
I wrote:
Longitudinal studies [longitudinal studies follow the same individuals over time, while cross-sectional studies investigate a group of individuals, but not necessarily the same individuals, at one or more points in time] of kittiwake populations have revealed a great diversity in individual life histories within populations and large amounts of phenotypic variation among individuals for traits such as survival, sexual maturity, and reproductive output.
The concept of “quality” (of parents, eggs, or offspring) has been used to explain these large differences in individual life histories and lifetime reproductive success, and the concept is now pervasive in studies of the individual dynamics of seabirds. Since the concept of quality is still ill-defined and often leads to circular and/or a posteriori arguments (e.g., high-quality birds are defined as birds with high reproductive success and vice versa), we do not model possible differences in “quality”.
The circular reasoning says that talent is what makes you better at, say, playing chess, and if you are better at chess (assuming most other things, such as time spent playing, age, etc., are equal), it means you are more talented at playing chess.
But, and this is the crucial question, without observing chess performance, can we identify chess talent? In some cases, it is possible to have an "intuition" for the expected performance; for example, there are no potential top-level sprinters who have short Achilles tendons—the Achilles of top international sprinters are either long or medium.
A high IQ (say, an IQ observed in only 0.01% or 0.001% of the population) seems to be a prerequisite for doing jobs that revolutionize a field in one of the hard sciences (mathematics, physics, chemistry, etc.), but it is far from being an incontrovertible predictor of professional success (although it has been found to be the best one); "they have the talent to be the best, but neither the energy nor the desire," is an observation about someone that I am sure many of us have heard.
IV.
I often interview candidates for open positions in my line of work in the technology sector. Typically, candidates face five or more interviews of an hour each, where they are asked "hard" questions (solving algorithmic problems or choosing between different machine learning solutions when, for example, we want to predict the time of arrival of a taxi) and "soft" or behavioral questions ("do you like working in a team?"). Like anyone else who conducts interviews, I want to check whether candidates are "talented" or not, but the typical interview questions that candidates can prepare for bore me to death: where's the fun in that?
Getting back to the podcast on "talent" that I listened to a few days ago, one of the authors of the book said that beyond the typical qualities one looks for when interviewing candidates, such as whether they are competent in the job they are applying for, he looks for people who are resilient and tenacious, and who possess unusual energy. He also finds that obsessiveness and competitiveness often correlate with talent. These are all points that I agree with.
But there is something else I look at when I interview candidates (and not only there), something I have found to be positively correlated with almost all excellence in human endeavors: curiosity about the world and a desire to find some kind of "solution" to problems—I much prefer those who take action to those who like to comment after the fact but do no actions.
The main question I use to assess this curiosity and problem-solving disposition in candidates is about movies: "I won't judge you on your taste in movies" is a line I use to calm their nerves. I ask:
How many movies do you think are shown in U.S. theaters in a (recent, pre-COVID) year?
Some candidates answer 100 or 1000 or 5000 without explaining how they got to those numbers. A quick answer that comes without an explanation is a "red flag" to me because, first, quick and intuitive answers are usually wrong, and second, where is the curiosity and desire to find a solution even with only a few pieces of the puzzle are available?
When the candidates, as it often happens, answer quickly and are inevitably wrong, I ask them how they arrived at that number. And, more often than not, they don't know—"maybe from up there", I often think.
At that point, I make it clear that I am not looking for a correct answer, but am interested in their reasoning, and in the structure of it: how did they get to that number?
I also understand very well that the candidates are under pressure—a pressure they are unlikely to feel when they do the actual work they are applying for—and so I give them plenty of time to think and reflect: "there is no urgency, we are all professionals," I like to tell them.
If you think about it, it is not that challenging to give a reasonable answer to my question. There are 52 weeks in a year, and how many new films do you see each week when you walk by a movie theater? Maybe five or six? That would give about 250-300 films a year. But then, one should think, there is always something we don't see: for every one person who does drugs in public, there are 5 who do drugs in private; for every war that is shown in the news, there are 3 or 4 that are raging but are not talked about by the general public.
It should not take a moment of genius for the candidate who is curious about the world to think of applying a correction, of using a multiplication factor, to the first data point to account for indie or low-budget or local productions that are shown in theaters, but may go unnoticed.
Should we use a factor of 2, 3, or 4? These are all reasonable assumptions and would speak highly of the candidate, who would be someone who observes ("I see 5 or 6 new films a week when I pass by movie theaters"), reflects on the hidden nature of most of the activities and events ("what we see is usually less than what is there") and then makes a reasonable assumption about the multiplication factor ("films to be shown in theaters are expensive to make, there can't be 10 indie films shown in theaters for every studio film"). The "correct" answer is about 750-800. But if they tell me, after explaining their reasoning, that 400 or 1200 movie are shown in each year, I still consider them excellent answers. I am not looking for the correct (but it better be reasonable) answer, just for curiosity and good thinking.
And this curiosity about the world, this desire to understand more and the passion for "solving problems," even or in particular when limited information is available, give a bright light to our existence. When we are curious and solution-driven, cooking meals moves from being a chore to a series of challenging and gratifying experiments; visiting a foreign country is not only looking at the usual 25 churches of other places of worship and endless bus rides to look at palaces built three centuries back, but also becomes an adventure in trying to “get by”, in finding a way in a foreign land to get the best table at a restaurant or meeting up with some local people who can introduce us to the real life of the “common folks” who live there; the act of writing, who at times can be boring and frustrating, can become much more attractive and adventurous when we ask ourselves: "I would love to talk about the seabirds I have studied for so many years and also about the circularity of reasoning about individual quality. How can I fulfill these desires when I write about talent after being inspired by a podcast on this topic that I listened to on my way to work?”
Italiano
I.
Qualche giorno fa ho ascoltato un podcast in cui i due ospiti parlavano di "talento" e, in particolare, di come riconoscere il talento—le persone intervistate di recente hanno scritto un libro proprio su questo argomento.
Si può definire talento una persona che sa fare particolarmente bene qualcosa o ha il potenziale per farlo, o un tratto, un'abilità o una caratteristica particolare che è di gran lunga migliore di quella che gli altri di solito possiedono; possiamo dire sia "lei è un talento" che "ha talento per il calcolo mentale".
Riconoscere il talento quando non è ancora pienamente espresso è compito arduo: chi ha praticato sport fin da giovane di certo ricorda decine di giovani atleti molto promettenti la cui carriera è evaporata come neve sotto il torrido sole di Luglio quando i ragazzi hanno raggiunto la pubertà, trovato una fidanzata che li ha fatti andare fuori di testa, o deciso di passare dal tiro in porta al tiro di cocaina.
Ci sono anche altre caratteristiche fisiche (la resistenza agli infortuni, per esempio) e psicologiche che non possono essere pienamente valutate quando i ragazzi sono ancora negli anni pre-puberali; ad esempio, è difficile capire quanto i ragazzi, da adulti, saranno in grado di sopportare la pressione della competizione quando ad essa parteciperanno dei professionisti—la pressione della competizione si sente poco quando il ragazzo promettente è dieci volte migliore degli avversari.
Per un talento che nasce una volta ogni cinquant’anni come Lionel Messi, ci sono centinaia di talenti che nascono una volta ogni cinquant’anni e però mai sbocciati perché i nervi li tradiscono quando scendono in campo. O rischiano di farsi male al solo soffio di un bacio in direzione dei loro polpacci.
II.
Al tempo delle mie ricerche di biologia evolutiva, un tratto o una caratteristica che ho a lungo studiato e mi interessava particolarmente era la "qualità individuale". Il concetto di qualità individuale è stato usato per spiegare l'eterogeneità inter-individuale delle prestazioni [performance, in termine tecnico]. In parole povere, ci sono individui che ottengono risultati migliori di altri individui, e questi individui sono per questo definiti di "qualità superiore". Ma mentre il raggiungimento di risultati migliori (avere più figli, sopravvivere per più anni, essere più grandi, più veloci, più resistenti) può essere constatato, la qualità intrinseca dell'essere migliori, al contrario, è spesso difficile, se non spesso impossibile, da osservare.
Ad esempio, potremmo pensare che avere degli figli nel corso della vita non sia un evento eccezionale (alla fine chi legge queste righe da qualcuno è pur nato), ma in molte specie, compresi gli esseri umani nel corso dei millenni, solo una frazione degli individui che raggiungono la maturità sessuale dà vita a prole che sopravvive anch’essa fino a riprodursi.
Per parlare di altre specie, solo il 30% circa degli uccelli marini adulti che ho avuto il piacere di studiare nelle mie ricerche biologiche è destinato a riprodursi con successo—ho usato l'avverbio "con successo" perché le uova possono essere fecondate, ma se dalle uova non escono pulcini o i pulcini muoiono subito (o vengono uccisi dai genitori!) dopo la schiusa, questi non contano per la continuazione della specie: si sono sì riprodotti, ma senza successo
E per offrire un ultimo esempio più facilmente osservabile, non possiamo dire se un uomo alto un metro e cinquanta centimetri sia alto o basso se non nel contesto della frequenza di una particolare statura nella popolazione: un uomo alto un metro e cinquanta centimetri è basso tra gli olandesi, ma è alto tra i pigmei.
Quando si osserva un fenomeno o un processo, è sempre utile—anzi necessario, ma iniziamo con il più tenue "utile"—studiare la sua distribuzione (qual è la frequenza degli eventi, delle misure, dei tratti?), grazie al quale possiamo osservare la realizzazione di un certo fenomeno nel contesto di ciò che può accadere e di quanto è probabile che accada.
Molte delle discussioni su chi sia il migliore tra gruppi di persone (più veloce, più alto, più intelligente, più abile) non vanno da nessuna parte, sono chiacchiere inutili, perché i partecipanti non ragionano in termini di distribuzioni.
Dire "gli uomini sono più alti delle donne" è intuitivamente vero, ma non significa che ogni uomo siano più alto di ogni donna: l'intuizione riguarda la media (gli uomini sono “in media” più alti delle donne) o l'aspettativa che si ha pensando a un uomo e a una donna presi a caso, con l'uomo che si prevede, cioè ci si aspetta, sia più alto della donna.
Nella figura seguente, che ho preso da Our World in Data e si riferisce all'altezza di uomini (in rosso) e donne (in blu) adulti nati tra il 1980 e il 1994 in Nord America, Europa, Asia orientale e Australia, le due distribuzioni di frequenza delle altezze si sovrappongono, e anche ampiamente.
Nella regione di sovrapposizione delle distribuzioni di altezza di uomini e donne, la stessa altezza può essere trovata sia negli uomini che nelle donne, sebbene la loro frequenza sia differente. Ad esempio, solo il 2,5% circa delle donne è più alta di 179 cm, ma il 50% degli uomini è più alto di 179 cm.
L’altezza di uomini e donne prese singolarmente (ma non quando sono prese insieme, in quel caso osserveremmo una distribuzione bimodale) segue una distribuzione normale, una forma molto comune, per ragioni matematiche, di distribuzione di probabilità.
La distribuzione normale è simmetrica, il che significa che, ad esempio, le persone che sono tra il 10% e il 15% più alte o tra il 10% e il 15% più basse dell'altezza media appaiono nella popolazione con la stessa frequenza.
Possiamo anche dire, perché questa è una proprietà delle distribuzioni normali, che il 95% delle altezze si trova entro 2 deviazioni standard dalla media. La distribuzione delle altezze degli uomini è più estesa di quella delle donne; questo si osserva tipicamente per una serie di tratti fisici e comportamentali, cioè lo stesso tratto è di solito più variabile negli uomini che nelle donne.
Poiché l'altezza media dei maschi in Nord America, Europa, Asia orientale e Australia nati tra il 1980 e il 1994 è di 5 piedi e 10 pollici (178,4 cm per chi non vive negli Stati Uniti) e la deviazione standard è di 3 pollici (7,6 cm), significa che solo il 2,5% dei maschi adulti negli Stati Uniti è più alto di 6 piedi e 4 pollici (193,6 cm) e solo il 2,5% è più basso di 5 piedi e 4 pollici (163,2 cm).
Le distribuzioni di probabilità normali o altre distribuzioni simmetriche ben descrivono la distribuzione di molti eventi comuni, ma sono comuni anche le distribuzioni di tipo power-law [legge di potenza] (o simili a una distribuzione power-law, qui sono più interessato all’intuizione, all’idea, che al dettaglio matematico). Mentre una distribuzione normale è simmetrica, il che implica che una differenza proporzionale dalla media in entrambe le direzioni è ugualmente probabile—essere più bassi di 163 cm e più alti di 193 è ugualmente probabile, dal momento che entrambe le misure si trovano a 2 deviazioni standard dalla media—una distribuzione power-law implica invece che una piccola quantità di eventi (o di episodi o oggetti o misure di qualche tipo) è comune, mentre eventi più grandi, forti o intensi sono rari.
Come mostrato nella figura sotto relativa alla distribuzione del reddito nelle famiglie statunitensi (i dati sono del 2014), il reddito o la ricchezza seguono una distribuzione power-law: ci sono pochissimi miliardari e molte persone che tirano a campare. E la distribuzione power law ben descrive anche la distribuzione di frequenza dell’intensità dei terremoti: molti sono i terremoti il cui verificarsi è rilevato solo da speciali strumenti e pochissimi sono i terremoti che radono al suolo una città.
Allo stesso modo, sono tante le donne che non si riproducono o fanno 1 o 2 figli, e poche quelle che nel corso della loro vita ne fanno 15 o 20.
Anni fa studiai le abitudini riproduttive di alcune popolazioni di pesci d'acqua dolce che, dopo anni di indagini scientifiche, conoscevo meglio dei miei vicini di casa. Con mia buona sorpresa, scoprii che dopo un'alluvione che aveva ucciso la maggior parte dei pesci adulti, una coppia di pesci diede vita, è proprio il caso di dire, all'80% dei piccoli nati uno e due anni dopo l'alluvione, mentre cinque o sei altre coppie di pesci produssero il restante 20%: pochi fanno tanto e tanti fanno poco.
Tutti gli organismi, a parte qualche eccezione (vedi il comportamento eusociale delle api), "desiderano" raggiungere la maturità sessuale e poi riprodursi; dopo aver perso la capacità riproduttiva, a causa della senescenza ad esempio (usando termini più comuni potremmo dire “dopo essere diventati vecchi”, ma ormai di vecchiaia non si muore nemmeno di più, si muore invece di patologie multiple) non fanno granché per la continuazione della specie.
Sono state fatte molte ricerche, e molte saranno fatte in futuro, per capire perché le donne sopravvivono ancora per parecchi anni dopo essere entrate in menopausa (o perché la menopausa esiste). La selezione naturale agisce su tratti che aumentano la fitness (cioè la capacità di sopravvivere, raggiungere la maturità sessuale, e riprodursi) dell’individuo o della specie, ma non dovrebbe, in teoria, agire su tratti che favoriscono la sopravvivenza dell’individuo dopo che esso ha perso la capacità riproduttiva (o agire per l’eliminazione di mutazioni deleterie che compaiono o hanno effetto nella tarda stagione della vita). A chi è interessato a saperne di più, consiglio di documentarsi sulla “ipotesi della nonna” [grandmother hypothesis].
III.
Si ritiene generalmente che il talento, il "talento intrinseco", cioè quello che ci viene dato dai nostri genitori e dalle esperienze dei primi anni di vita, sia normalmente distribuito nella popolazione, ma che i successi seguano invece una distribuzione power-law, con molti che ottengono poco o nulla e altri, pochi, che giocano nei massimi campionati per 12 anni vincendo un gran numero di anelli e medaglie.
Esistono certamente differenze notevoli di abilità o qualità tra le persone per una specifica attività: è sotto gli occhi di tutti che ci siano persone “naturalmente” più portate di altre nel disegno artistico, ad esempio. Non sono tra quelli.
Alcune persone sono più dotate della maggior parte dei loro pari non in una, ma in molte attività o qualità, alcune delle quali non ci si aspetta siano, a prima vista, correlate positivamente (in generale, c'è una correlazione positiva tra due misure quando all’aumentare di una anche l’altra aumenta, ma questo non significa necessariamente che una causi l’altra): per esempio, essere attraenti e intelligenti e generosi. “Avete bisogno di qualcos’altro?”, viene da chiedere a questi fortunati.
L’esistenza di queste correlazioni positive non casuali è piuttosto controintuitiva, poiché per ragioni culturali— e direi anche per un messaggio comune a tutte le religioni—tendiamo a credere che ciò che viene dato in un tratto, in un'abilità o in una qualità, venga tolto ad altri tratti o altre qualità. In questo senso, non ci aspettiamo che la bella donna sia anche molto intelligente e ci aspettiamo che chi ha avuto la sventura di trovarsi in sedia a rotelle sia una persona migliore, in linea di massima, di chi può camminare.
Ma questo non ha alcuna base empirica, non lo osserviamo, lo pensiamo e forse, a volte, lo speriamo. Ci sono molti uomini e donne bellissimi che sono anche terribilmente intelligenti. E direi che mi aspetto che questa combinazione sia più probabile rispetto a belli e tonti e bruttini e brillanti, poiché il "talento" o l'ingrediente comune alla base di entrambe le "qualità" bellezza-intelligenza è la "salute".
Dall’altro lato, ci sono molte persone terribili che hanno avuto la sfortuna non solo di essere pessime, ma anche di non poter camminare e di essere perciò costrette su una sedia a rotelle: la vita non è giusta, e il concetto di "giustizia" è puramente culturale— “chi ha sete di giustizia, avrà poco da bere”, avrei voluto trovare scritto nella Bibbia. Infatti, se passiamo dagli esseri umani ai leoni, mettiamo, non ci aspettiamo che i leoni fragili, malandati che sono stati storpiati da un bufalo in una cruenta battaglia per la cena siano "saggi", "gentili" o "buoni conversatori".
Ai massimi livelli di qualsiasi attività, e soprattutto quando i risultati sono misurabili (ad esempio, peso, secondi, distanza, o il plauso degli esperti) e dipendono dall'individuo (non c'è lavoro di squadra!), tutti i concorrenti hanno un "talento intrinseco", probabilmente una combinazione di geni e di positive esperienze precoci, quelle dei primissimi anni di vita: posso allenarmi quanto voglio, ma non sarò mai veloce in una gara di 100 metri come un concorrente di livello nazionale, semplicemente non ho il "talento" per farlo. Potrei diventare migliore di quello che sono (o meglio, avrei potuto essere migliore di quanto sono stato) senza alcun dubbio, ma il livello nazionale, per non dire internazionale, è e sempre fu al di fuori delle mie possibilità. Allo stesso modo, piazzarsi alle Olimpiadi di matematica o fisica è impossibile per persone senza i geni giusti, e purtroppo io questi geni giusti non li ho (ma la vita è entusiasmante anche quando privi di quei geni).
Il problema principale quando si parla di "talento" o "qualità" è che la maggior parte delle discussioni su questo argomento sono circolari, e ne ho scritto in una vecchia bozza di un articolo che ho poi pubblicato sulle storie di vita dei kittiwake (un comune uccello marino). Scrissi:
Gli studi longitudinali [gli studi longitudinali seguono gli stessi individui nel tempo, mentre gli studi con campionamenti trasversali analizzano una popolazione o un gruppo di individui, ma non necessariamente gli stessi individui, ad uno o più punti nel tempo] sulle popolazioni di kittiwake hanno rivelato una grande diversità nelle storie di vita individuali all'interno delle popolazioni e una grande quantità di variazione fenotipica tra gli individui per tratti come la sopravvivenza, la maturità sessuale e la riproduzione.
Il concetto di "qualità" (dei genitori, delle uova o della prole) è stato usato per spiegare queste grandi differenze nelle storie di vita individuali e nel successo riproduttivo nell'arco della vita, e il concetto è ora pervasivo negli studi sulle dinamiche individuali degli uccelli marini. Poiché il concetto di qualità è ancora poco definito e spesso porta ad argomentazioni circolari e/o a posteriori (ad esempio, uccelli di alta qualità definiti come uccelli con alto successo riproduttivo e viceversa), non modelliamo le possibili differenze in "qualità".
Il ragionamento circolare è quello che dice che Il talento è ciò che vi rende migliori, ad esempio, nel gioco degli scacchi, e se siete più bravi negli scacchi (supponendo che la maggior parte delle altre variabili, come il tempo trascorso a giocare, l'età ecc. siano uguali) avete più talento. Ma, e questa è la domanda cruciale, senza osservare le prestazioni scacchistiche, possiamo identificare il talento per gli scacchi?
In alcuni casi, è possibile “intuire" il talento; per esempio, non esistono potenziali velocisti di alto livello che abbiano i tendini d'Achille corti—gli Achillei dei migliori velocisti internazionali sono lunghi o medi. Un elevato quoziente intellettivo (ad esempio, un QI osservato solo nello 0.01% o 0.001% della popolazione) sembra essere un prerequisito per svolgere lavori che rivoluzionano certi campi delle scienze dure (matematica, fisica, chimica ecc.), ma è ben lungi dall'essere un predittore incontrovertibile di successo professionale (anche se è decisamente il migliore che abbiamo): "ha il talento per farlo, ma non ha né l'energia né il desiderio", è una frase che abbiamo ascoltato più di una volta.
IV.
Mi capita spesso di condurre colloqui con candidati che si propongono per posizioni aperte nel mio settore di lavoro, quello della tecnologia. In genere, i candidati devono sostenere cinque o più colloqui di un'ora ciascuno, in cui vengono poste domande "difficili" (risolvere problemi algoritmici o scegliere tra diverse soluzioni di machine learning quando, ad esempio, vogliamo predire qualcosa come il tempo di arrivo di un taxi) e domande "morbide" o comportamentali ("ti piace lavorare in gruppo?"). Lo scopo del mio e degli altri colloqui è quello di valutare se i candidati siano "talentuosi" o meno, ma mi annoia tremendamente porre le tipiche domande alle quali i candidati si sono già preparati a rispondere: dov'è il divertimento per me?
Tornando al podcast sul "talento" che ho ascoltato qualche giorno fa, uno degli autori del libro ha affermato che, al di là delle qualità tipiche che si cercano nei candidati, come ad esempio la competenza nel lavoro per il quale si stanno proponendo, lui cerca persone che siano resistenti e tenaci, e che abbiano un'energia fuori dal comune. Inoltre, trova che l'ossessività e la competitività siano tratti spesso correlati al talento. Sono posizioni che condivido.
Ma c'è qualcos'altro che valuto quando conduco i colloqui (e non soltanto lì), un tratto che ho scoperto essere positivamente correlato con quasi tutte le eccellenze nelle attività umane: la curiosità per il mondo e il desiderio di trovare qualche tipo di "soluzione" ai problemi—preferisco di gran lunga chi si lancia anche alla garibaldina a chi commenta dopo il fatto.
La domanda principale che uso per valutare questa curiosità e la disposizione alla soluzione dei problemi nei candidati è sui film: “La mia valutazione non dipende dai tuoi gusti cinematografici" è una battuta che uso per calmare i loro nervi.
Chiedo:
"Quanti film pensi che vengano proiettati nelle sale cinematografiche degli Stati Uniti in un anno (recente, pre-COVID)"?
Alcuni candidati rispondono 100 o 1000 o 2000, senza spiegare o discutere come siano arrivati a quel numero. Una risposta rapida e non accompagnata da un ragionamento è per me un “campanello d’allarme” perché, in primo luogo, le risposte rapide e intuitive sono in genere errate e, in secondo luogo, dov'è la curiosità e il desiderio di trovare una soluzione anche con pochi tasselli del mosaico a disposizione?
Quando rispondono in modo rapido e inevitabilmente sbagliato, chiedo loro come siano arrivati a quel numero. E, il più delle volte, nemmeno loro lo sanno —”forse un intervento divino”, penso io.
A quel punto, chiarisco che non sto cercando una risposta corretta, ma sono interessato al loro ragionamento, alla struttura della loro indagine. Capisco anche bene che i candidati sono sotto pressione—una pressione che difficilmente proveranno quando svolgeranno il lavoro vero e proprio per il quale si candidano—e quindi lascio loro tutto il tempo per pensare e riflettere: “non c’è urgenza, siamo tutti professionisti”, sono solito dire.
Se riflettete un minimo, non è poi così difficile dare una risposta sensata. Ci sono 52 settimane in un anno, e quanti nuovi film vedete ogni settimana quando passate (se non ci passate mai, su un po’ di vita) davanti a dei cinema ? Forse cinque o sei? Questo darebbe circa 250-300 film all'anno. Ma poi, viene da pensare, c'è sempre qualcosa che non vediamo; per ogni persona che si droga in pubblico, ce ne sono 5 che si drogano in privato; per ogni guerra che viene mostrata nei telegiornali, ce ne sono 3 o 4 che infuriano con la povera gente che salta per aria a destra e a sinistra, ma di cui il grande pubblico non parla.
Ne consegue che il candidato curioso del mondo non deve essere un genio per pensare di applicare una correzione, un fattore di moltiplicazione, ai primi dati (i 250-300 film) per tenere conto delle produzioni indie o a basso costo o locali. Dovremmo moltiplicare per 2, 3 o 4?
Sono tutte ipotesi ragionevoli che metterebbero in buonissima luce il candidato, il quale pertanto si presenterebbe come una persona che osserva ("vedo che 5 o 6 nuovi film in totale vengono mostrati in un paio di multisala ogni settimana"), riflette sulla natura nascosta della maggior parte dell'attività ("quello che vediamo è di solito meno di quello che esiste") e poi avanza un'ipotesi ragionevole sul fattore di moltiplicazione ("i film da proiettare in sala sono costosi da realizzare, non credo ci siano 10 film indie proiettati in sala per ogni film prodotto dagli studios"). La risposta "corretta" sarebbe circa 750-800 film proiettati un anno, questi erano i numeri prima del 2020. Ma se, dopo aver spiegato il ragionamento, il candidato mi rispondesse con 400 o 1200 film proiettati ogni anno, le considererei comunque eccellenti risposte. Non sono interessato alla risposta esatta (ma almeno ragionevole sì), ma alla curiosità e al ragionamento.
E questa curiosità per il mondo, questo desiderio di capire di più e la passione per "risolvere i problemi", anche o soprattutto quando le informazioni disponibili sono limitate, accendono una luce brillante sulla nostra esistenza.
Quando siamo curiosi e orientati alla soluzione, la preparazione dei pasti in cucina passa dall'essere un lavoro di routine a una serie di esperimenti stimolanti e gratificanti; visitare un Paese straniero è non solo ammirare le solite 25 chiese o altri luoghi di culto e interminabili viaggi in autobus per controllare edifici costruiti tre secoli fa, ma diventa anche un’avventura nel cercare di arrangiarsi, nel trovare il modo in terra straniera di ottenere il tavolo migliore in un ristorante o di incontrare qualche locale che possa introdurci alla vita reale delle persone che vivono lì; l'atto di scrivere, che a volte può essere noioso e frustrante, diventa più interessante quando ci chiediamo: "vorrei tanto parlare degli uccelli marini che ho studiato per anni e della circolarità del ragionamento sulla qualità individuale, come posso soddisfare questi desideri mentre scrivo di talento partendo da un podcast sullo stesso tema che ho ascoltato mentre andavo al lavoro?"